深入理解 VGG 卷积神经网络
VGG 网络是一种经典的图像分类网络,通过多层卷积操作提取图像特征实现图片分类。由于能够提取图像的特征,也应用于风格迁移网络中的损失函数。另外用于边缘检测的 HED(Holistically-Nested Edge Detection) 网络也是基于 VGG 网络发展而来。 VGG 名称来源于作者所在的牛津大学视觉几何组(Visual Geometry Group)。
本文主要分析 VGG 网络的结构,从结构出发了解网络各层的作用,数学原理,以及 TensorFlow 实现。
根据卷积层数及参数的不同,VGG 网络有以下不同的结构:
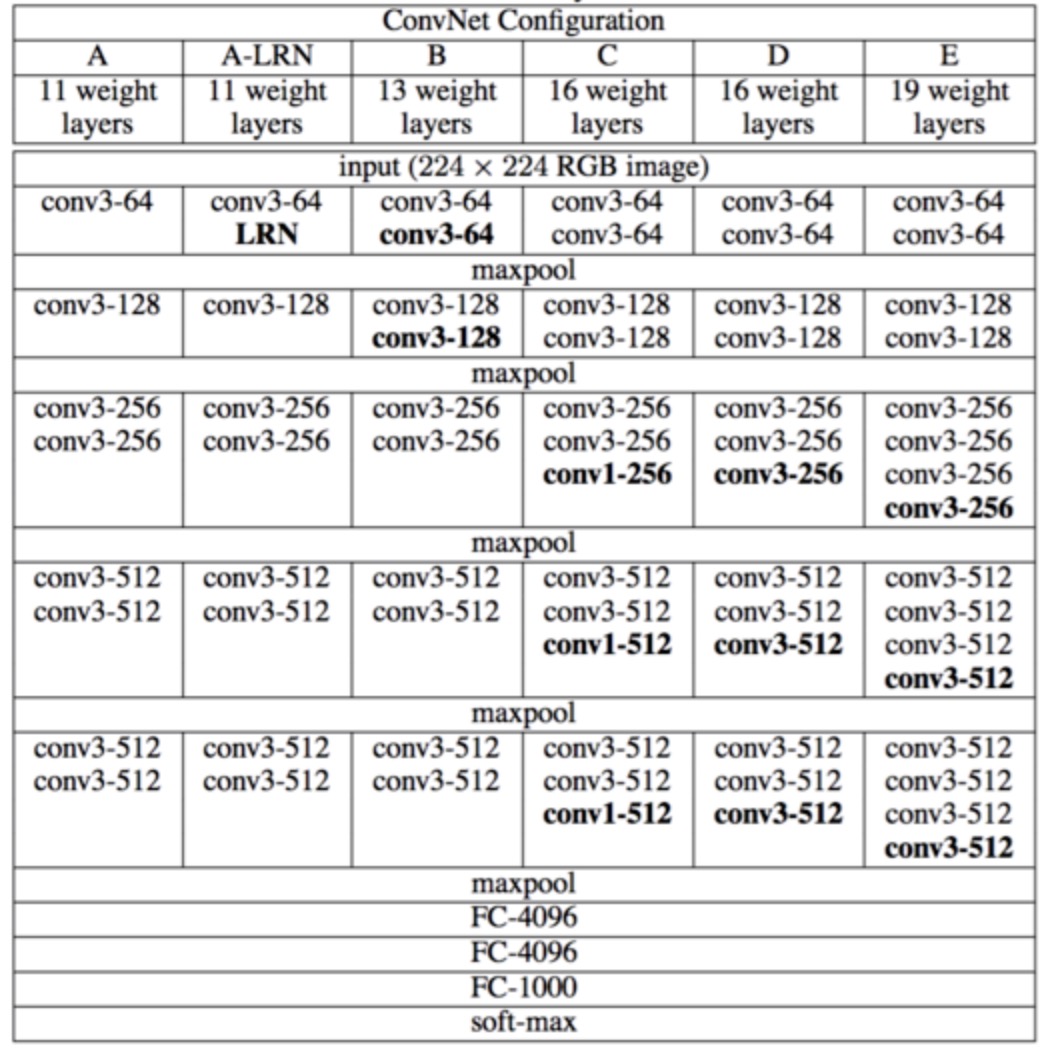
较常使用的是 VGG-16 与 VGG-19,其中16、19代表的是去除了池化层(maxpool) 与 softmax 层之后的网络层数,其中 VGG-19 比 VGG-16 多了 3 个卷积层。
下图展现了 VGG-16 图像分类网络的结构:
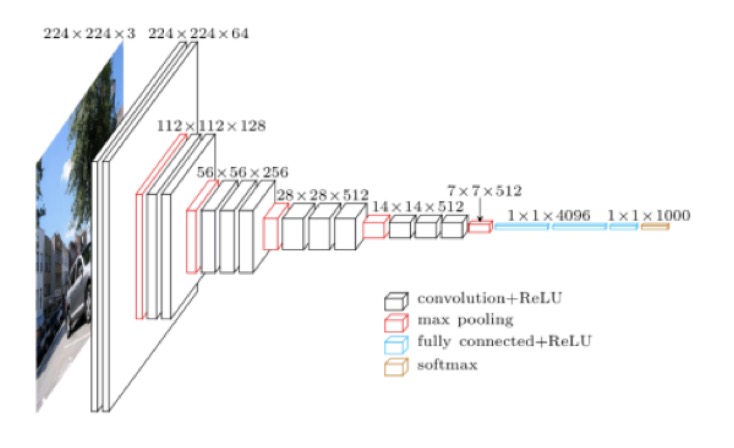
从右下角的图例可以看出 VGG-16 图像分类网络主要包含了 4 类层级:
- convolution + ReLU : 卷积层提取特征,ReLU 为激活函数 max(0, x)
- max pooling: 最大池化层
- fully connected + ReLU: 全连接层
- softmax:用于输出最终各分类结果的概率分布
卷积层
先从卷积层入手,那么何为卷积?我们称 (f * g)(n) 为 f, g 的卷积,在离散空间下有如下定义:
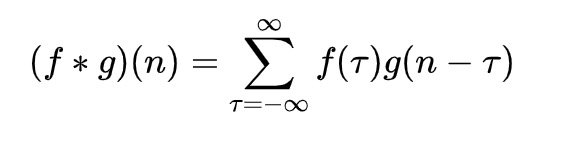
以掷骰子为例,求两枚骰子掷出和为 4 的概率,f(x) 表示第一个骰子掷出 x 的概率,g(x) 表示第二个骰子掷出 x 的概率,那么 P = f(1)g(3) + f(2)g(2) + f(3)g(1)。以卷积的形式表示为:
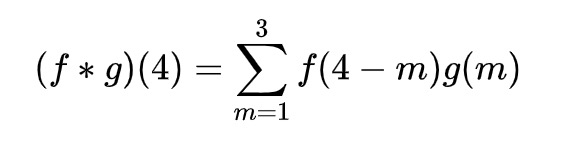
矩阵的卷积稍有不同,通常有一个称为卷积核(也称为过滤器)的矩阵 w,步长为 1 针对矩阵 a 进行卷积,过程如下:
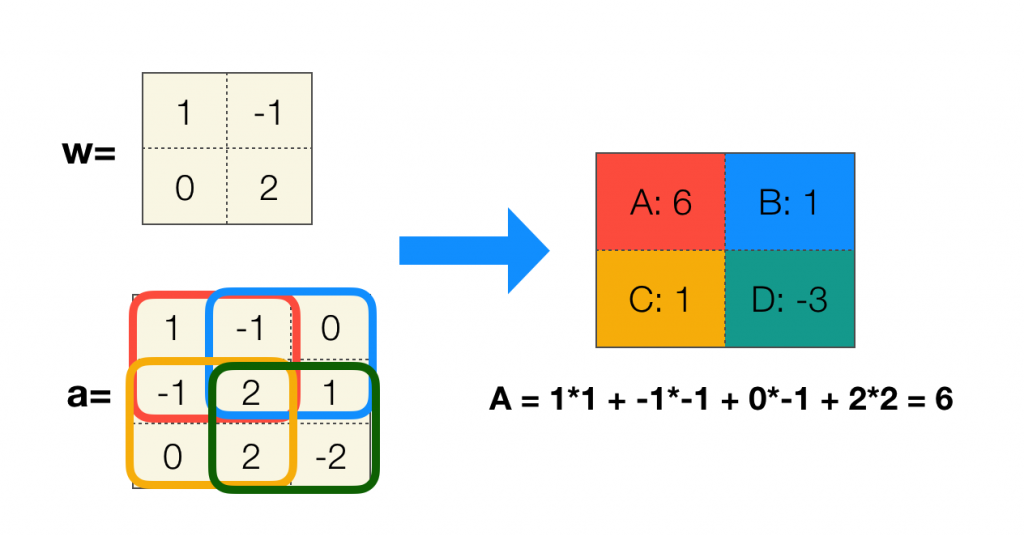
这里还有一个小细节,还记得离散卷积公式中的 n 吗,卷积过程中有个不变量,矩阵卷积中这个不变量是下标和,为了更直观并且方便计算,w 其实已经将卷积核上下翻转 180° 了,以达到下标和为 (1, 1) 的效果。

那么矩阵卷积的公式可以对应为:
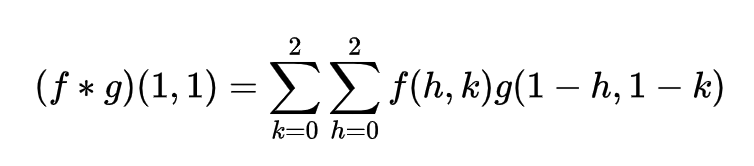
为了不让卷积操作减小原矩阵的尺寸,可以在输入矩阵的边界加入全 0 填充(zero-padding),这可以使得输出矩阵与输入矩阵尺寸保持一致。
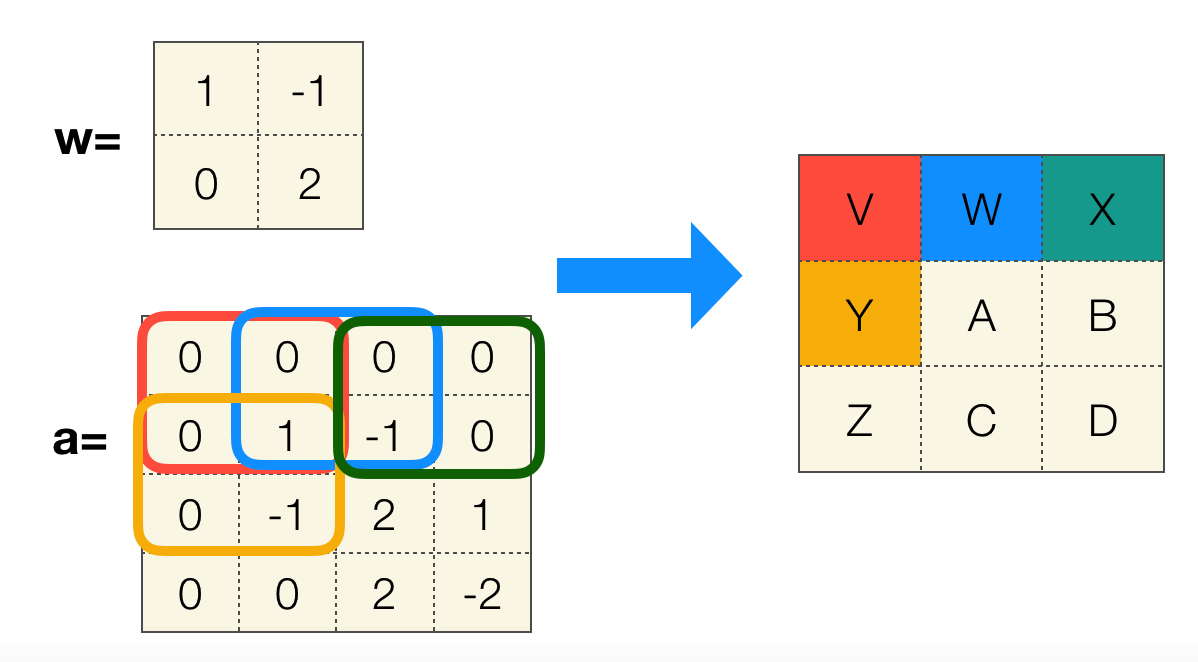
当然步长也会影响最终卷积结果的尺寸:
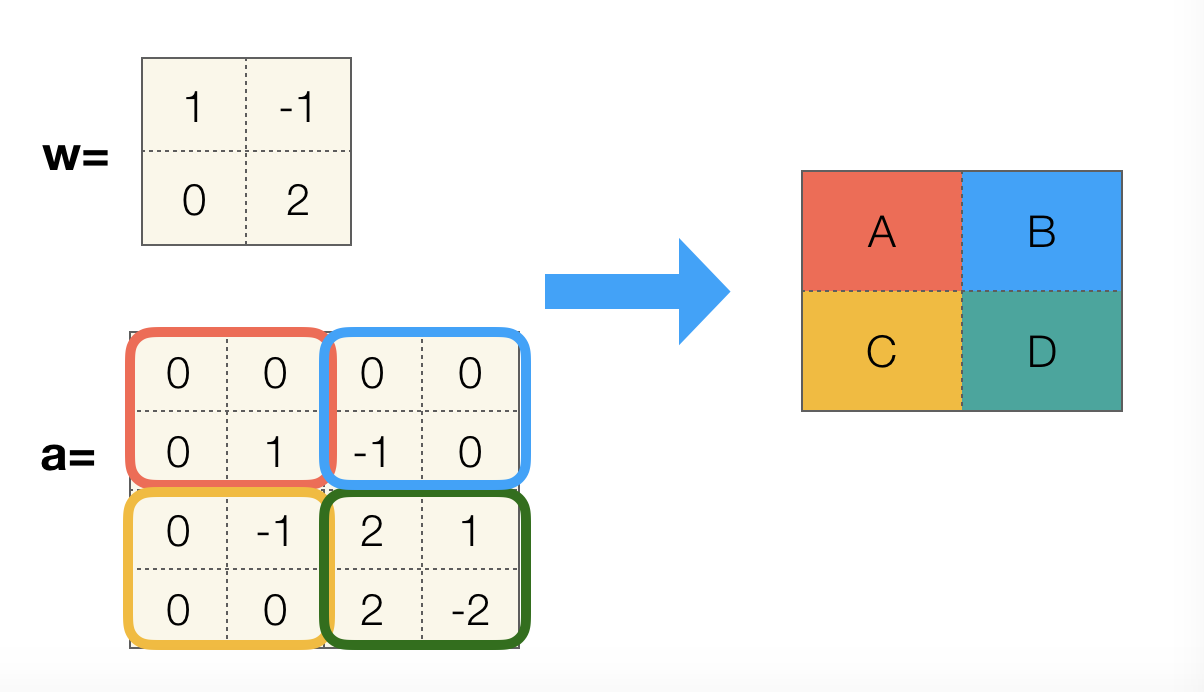
那么如果不使用全 0 填充,输出矩阵的尺寸由卷积核尺寸与步长共同决定:
out-length = (in-length – filter-length + 1) / stride-length
Tensorflow 可以方便的实现卷积层:
filters = tf.truncated_normal([3, 3, in_channels, out_channels], 0.0, 0.001)
biases = tf.truncated_normal([out_channels], .0, .001)
conv = tf.nn.conv2d(input=bottom, filter=filters, strides=[1, 1, 1, 1], padding='SAME')
bias = tf.nn.bias_add(conv, conv_biases)
relu = tf.nn.relu(bias)filters 声明的是一个四维矩阵,第一第二维代表卷积核(或者称过滤器)尺寸,第三维表示输入层的深度,第四维表示输出层的深度。biases 是个偏置量,每个深度对应一个偏置量,所以总共有输出层的深度个偏置量。
tf.nn.conv2d 实现了卷积层的向前传播算法,input 为输入矩阵,strides 为长度为 4 的数组,表示步长,因为步长只对矩阵长和宽有效,所以数组的第一位与第四位一般为 1 ,第二位与第三位表示步长。padding 参数为填充方法, SAME 表示全 0 填充, VALID 表示步填充。
然后卷积操作之后一般会加上偏置量,再通过激活函数输出给下一层。卷积层不改变矩阵的长宽,但每个区块的第一个卷积层会将矩阵的深度扩大一倍。
池化层
池化层主要作用是缩小矩阵尺寸,减少参数,起到了加速计算同时防止过拟合的作用。与卷积层类似,池化层也有一个类似过滤器的结构,并且也有步长的概念。池化层主要分为最大池化层(max pooling)和平均池化层(average pooling)。
下图展示了过滤器尺寸为 2*2,步长为 2,使用 0 填充的最大池化层过程:
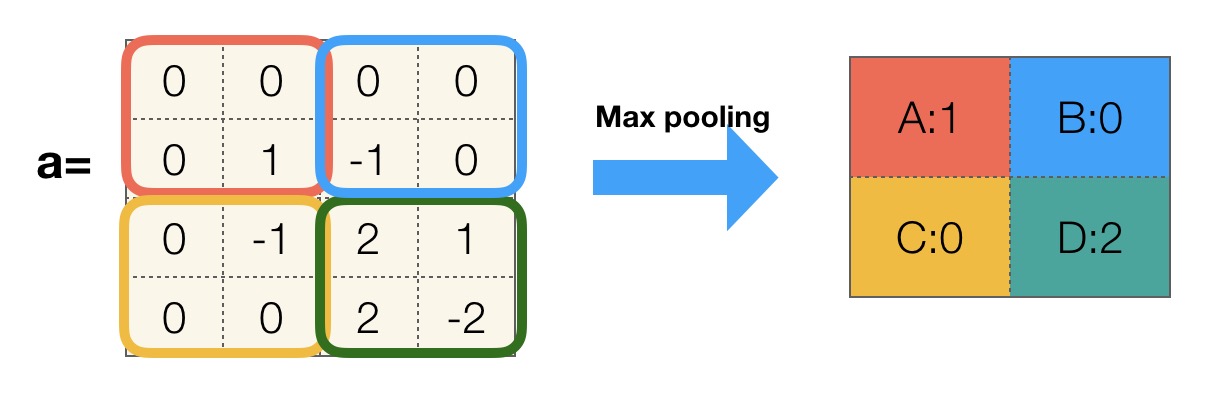
以下是 TensorFlow 实现的最大池化层向前传播算法:
tf.nn.max_pool(bottom, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME', name=name)ksize 表示的是过滤器尺寸,是个长度为 4 的数组,第一、四位为 1,strides 表示步长,同样的第一、四位为 1。padding=’SAME’ 表示使用 0 填充。这里虽然使用了 0 填充,但是步长为 2 ,所以最终输出尺寸会缩小。
池化层不改变矩阵的深度,但会将矩阵长宽缩小一倍。
全连接层
在整个卷积神经网络中卷积层和池化层是针对输入的特征提取,那么全连接层就起到“分类器”的作用。实现上比较简单,直接使用矩阵相乘即可。
两个矩阵相乘有以下尺寸特征:已知矩阵 X 尺寸为 (a, b),矩阵 Y 尺寸为 (m, n),矩阵 Z = X * Y。那么必须有 b == m,并且输出 Z 的尺寸为 (a, n)。
例如 VGG-16 中的第一个全连接层,输入尺寸为 (7,7,512),通过 tf.reshape 转换成 (1, 7*7*512) , 也就是 (1, 25088),矩阵乘另外一个大小为 (25088, 4096) 的矩阵,最终输出矩阵尺寸为 (1, 4096),用以下公式表示:
(1, 25088)*(25088, 4096) = (1, 4096)
使用 TensorFlow 实现以上逻辑:
weights = tf.truncated_normal([25088, 4096], 0.0, 0.001)
biases = tf.truncated_normal([4096], .0, .001)
x = tf.reshape(bottom, [-1, 25088])
fc = tf.nn.bias_add(tf.matmul(x, weights), biases)其中 bottom 为尺寸是 (7,7,512) 的输入矩阵,使用 tf.matmul 实现矩阵层的向前传播算法,然后再使用 tf.nn.bias_add 加上偏置量。需要注意的是在使用 tf.matmul 的时候小心和 tf.multiply 混淆,后者是矩阵点乘。
Softmax 回归
Softmax 一般用于分类问题,也可以算作是一种激活函数,作用是将最后输出结果转换为归一化的概率分布。数学公式表示为:
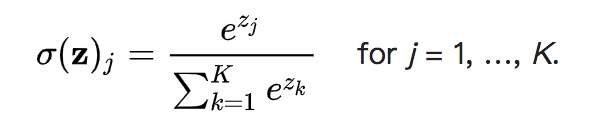
对于输入向量 [1, 2, 3, 4, 1, 2, 3] 对应的 Softmax 函数的值为 [0.024, 0.064, 0.175, 0.475, 0.024, 0.064, 0.175]。从效果上来看和每一项除以总和有点类似,之所以在公式中引入自然参数 e 是为了凸显其中最大的值并抑制远低于最大值的其他分量。
TensorFlow 中的实现如下:
prob = tf.nn.softmax(fc8, name="prob")激活函数
我们经常会使用激活函数来去除模型的线性化,让网络可以使用更少的参数抽象更复杂的模型,常见的激活函数有 sigmoid函数、tanh函数、relu函数。
VGG-16 中使用 relu 作为激活函数,数学表示为:
relu = max(0, x)
sigmoid 与 tanh 函数的几何图像分别如下:
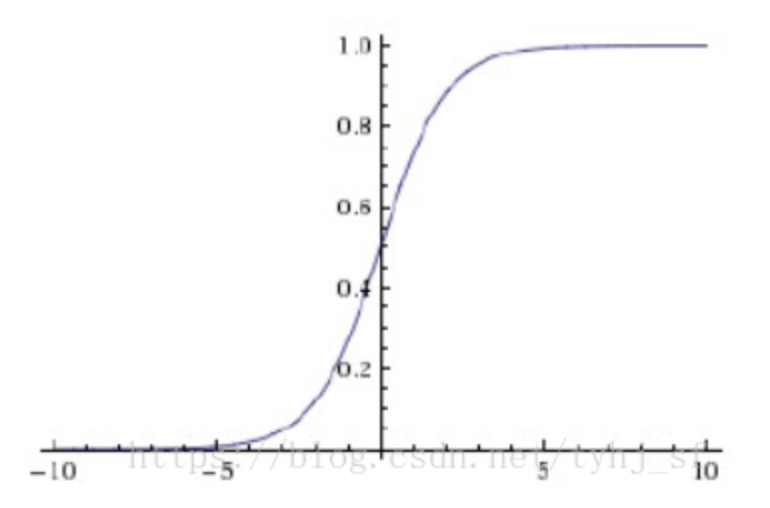
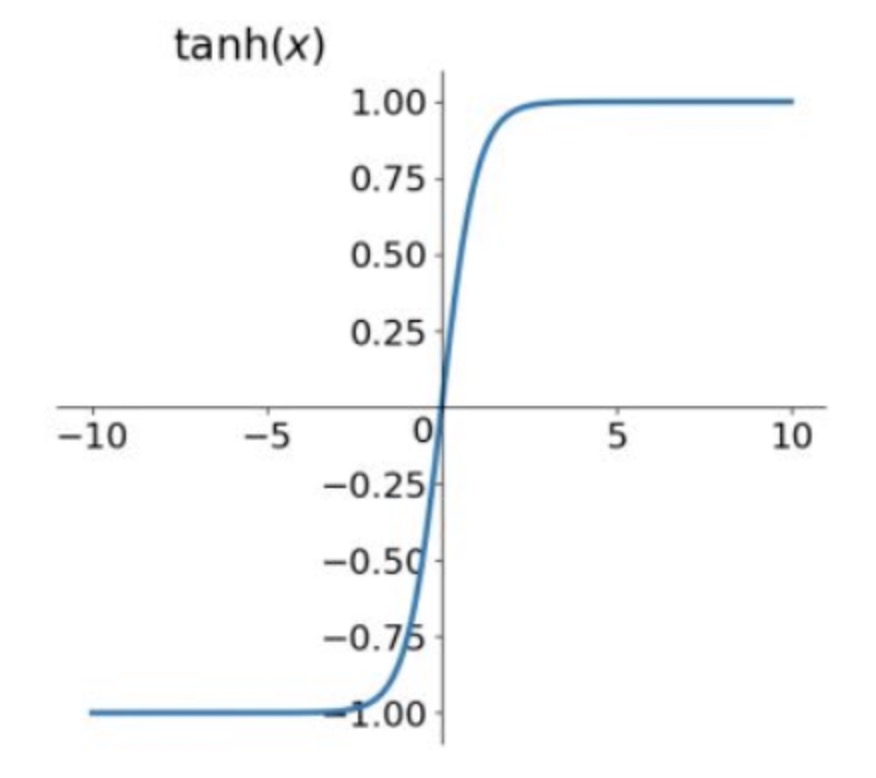
需要注意的是各激活函数的输出范围,比如 sigmoid 函数输出的范围是 (0, 1);tanh 函数输出范围是 (-1, 1)。
常用的激活函数在 TensorFlow 中也都有实现:
tf.nn.relu(bottom)
tf.nn.sigmoid(bottom)
tf.nn.tanh(bottom)VGG 网络实现
网络的具体实现就不在这里展开了,可以移步 Github 查看:tensorflow-vgg
由于 VGG-16 网络参数较多,大概有 1.38 亿个参数,所以一般情况下会加载训练好的分类模型做迁移训练。作者提供了训练好的分类模型参数供下载(npy 文件),可以先加载训练好的参数再进行训练可以大大减少训练时间。
其中全连接层的参数又占了整个网络参数的绝大部分,那么训练结果很容易依赖于局部权重出现过拟合问题,为了缓解过拟合问题,对第一层与第二层的全连接层做了 dropout 处理:
self.relu6 = tf.nn.dropout(self.relu6, self.dropout)
self.relu7 = tf.nn.dropout(self.relu7, self.dropout)dropout 函数会以一定的概率使得输入矩阵某些局部位置的权重失效,让模型不再依赖局部权重,缓解过拟合问题。
此外,正则化也是有效避免过拟合问题的手段。分为 L1 和 L2 正则化。L1 正则化为矩阵各权重的绝对值的和,L2 正则化为矩阵各权重的平方的和。将上述和加进最终训练的损失函数中,以到达避免权重过大的效果,使得模型不能任意拟合训练中的噪音。正则化对应的数学公式:
K(x) = J(x) + aR(w)
J(x) 为原损失函数(或称为目标函数),R(w) 对应 L1 或 L2 正则项,a 控制正则项的影响力。K(x) 为新的损失函数。
TensorFlow 实现如下:
weights = tf.constant([[1., -2.], [-3., 4.]])
l1_value = tf.contrib.layers.l1_regularizer(0.5)(weights)
l2_value = tf.contrib.layers.l2_regularizer(0.5)(weights)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
print(l1_value.eval())
print(l2_value.eval())L1 的输出值为 5.0 = (|1| + |-2| + |-3| + |4|)* 0.5 = 5.0;
L2 输出值为 7.5 = (1^2 + (-2)^2 + (-3)^2 + (4)^2) / 2 * 0.5,TensorFlow 实现的 L2 正则会将值除以 2。
例如在 VGG 网络中,可以将全连接层的权重的 L2 正则加入到集合中:
def fc_layer(self, bottom, in_size, out_size, name):
with tf.variable_scope(name):
weights, biases = self.get_fc_var(in_size, out_size, name)
x = tf.reshape(bottom, [-1, in_size])
fc = tf.nn.bias_add(tf.matmul(x, weights), biases)
// 全连接层权重计算 L2 正则,并加入集合中
tf.add_to_collection('l2-regular', tf.contrib.layers.l2_regularizer(0.5)(weights))
return fc在计算损失函数的时候通过以下方式取出集合,并加入到原损失中:
l2_value = tf.get_collection('l2-regular')原模型是 1000 分类的网络,经过最后一个全连接层,将输出长度为 1000 的一维数组:
self.fc8 = self.fc_layer(self.relu7, 4096, 1000, "fc8")如果自己训练模型的时候不需要支持这么多的分类,可以做出如下修改:
def build(self, rgb, train_mode=None):
// 略...
self.fc8 = self.fc_layer(self.relu7, 4096, self.num_class, "fc8")
// 略...
def get_var(self, initial_value, name, idx, var_name):
if self.data_dict is not None:
// 修改最后的全连接层权重取值,只读取前 num_class 个参数,而非全部的 1000 个
if name == 'fc8' and var_name == 'fc8_weights':
value = self.data_dict[name][idx][:, 0:self.num_class]
elif name == 'fc8' and var_name == 'fc8_biases':
value = self.data_dict[name][idx][:self.num_class]
else:
value = self.data_dict[name][idx]
else:
value = initial_value
//... 同原方法
return var一是修改最后一层全连接层的输出大小,二是修改加载 npy 文件时的逻辑,只读取前 num_class 个参数。



发表评论